

Los estudios de caso que utilizan el taper crítico en la geotecnia ilustran las aplicaciones prácticas y los resultados de este concepto en proyectos del mundo real. Estos estudios a menudo detallan los desafíos encontrados en proyectos específicos, como deslizamientos de tierra, inestabilidades de pendientes y la construcción de infraestructura en terrenos difíciles. Mediante la aplicación del análisis del taper crítico, los ingenieros pueden identificar las causas subyacentes de estos problemas y desarrollar soluciones dirigidas para mitigar los riesgos. Estos estudios de caso sirven como herramientas valiosas de aprendizaje para la comunidad de geotecnia, ofreciendo perspectivas sobre las complejidades de la estabilidad de pendientes y la efectividad de diversas estrategias de intervención.«¿Inteligente o hermosa? Evolución de la cuña acrecionaria vista como una competencia entre trabajo mínimo y cono crítico»
La teoría del Taper Crítico sugiere que en áreas costeras, los sedimentos se acumulan hasta un ángulo crítico antes de volverse inestables y provocar deslizamientos de tierra o fallas de pendientes. Esto puede tener varias implicaciones ambientales. En primer lugar, los deslizamientos de tierra pueden causar daños a la infraestructura, la propiedad y los ecosistemas. En segundo lugar, el movimiento de los sedimentos puede alterar el equilibrio sedimentario en las áreas costeras, afectando la erosión de las playas y las formas de las costas. Finalmente, los sedimentos generados por deslizamientos de tierra pueden ser transportados a cuerpos de agua, impactando potencialmente la calidad del agua y los ecosistemas marinos. La comprensión y gestión adecuadas del concepto de Taper Crítico son cruciales para minimizar estas implicaciones ambientales.«Resistencias de la corteza y fallas a partir de mediciones de cono crítico: insights sobre el comportamiento de cuñas acrecionarias usando modelos de elementos distintos - NASA/ADS»
| Escenario | Tipo de Material | Propiedades del Suelo | Rango de Profundidad (m) | Contexto Geológico | Taper Crítico (Grados) |
|---|---|---|---|---|---|
| Corteza Continental Estable | Roca Sedimentaria | Alta Resistencia a la Compresión | 70 - 1994 | Plataformas y Mesetas Continentales | 16 - 25 |
| Zonas de Subducción | Sedimento Rico en Arcilla | Baja Permeabilidad y Plasticidad | 673 - 2937 | Fronteras de Placas Convergentes | 6 - 14 |
| Líneas de Falla Activa | Sedimento Mixto | Tamaño de Grano Variable | 132 - 1366 | Fronteras de Transformación | 21 - 30 |
| Regiones Glaciares | Till Glaciar | Altamente Consolidado | 28 - 430 | Valles Glaciados y Fiordos | 10 - 19 |
| Áreas Volcánicas | Ceniza Volcánica | Porosa y Baja Densidad | 92 - 882 | Cerca de Volcanes Activos | 26 - 35 |
En conclusión, los estudios de caso en geotecnia utilizando el concepto de ángulo crítico han demostrado ser una herramienta valiosa en la evaluación de la estabilidad y seguridad de taludes, excavaciones y otras estructuras geotécnicas. Al considerar el ángulo crítico, los ingenieros pueden predecir los modos de falla potenciales y diseñar eficazmente medidas de mitigación para mejorar la estabilidad. Estos estudios de caso resaltan la importancia de incorporar el análisis del ángulo crítico en las prácticas de geotecnia para asegurar la seguridad y durabilidad a largo plazo de los proyectos de infraestructura.«Aplicación de modelado de elementos distintos al cono de cono crítico con heterogeneidad - NASA/ADS»
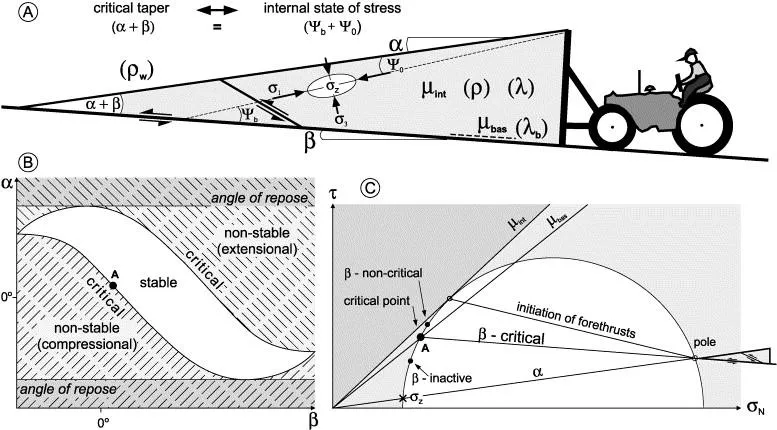
El análisis del ángulo crítico puede ayudar en los modelos de predicción de terremotos al proporcionar información sobre la estabilidad de las fallas y el potencial de deslizamiento. Al examinar el ángulo de corte de una falla, que es el ángulo en el que se encuentran los planos de falla, podemos determinar si está cerca o se desvía de la criticidad. Las fallas que se acercan al ángulo crítico son más propensas a producir terremotos, ya que hay una acumulación de estrés que podría resultar en un deslizamiento. Por lo tanto, monitorear los cambios en el ángulo de corte puede ayudar a identificar áreas de mayor riesgo sísmico y ayudar en la predicción de su ocurrencia.«Crecimiento dinámico y cinemático de una cuña de Coulomb»
La tecnología de teledetección puede utilizarse en el análisis del ángulo crítico al proporcionar datos valiosos sobre la distribución espacial y las características de las características geológicas. Estos datos pueden incluir topografía, rugosidad superficial, ángulo de pendiente e información sobre la cobertura del suelo, que son entradas esenciales en el análisis del ángulo crítico. Las técnicas de teledetección como LiDAR, imágenes satelitales y fotografía aérea pueden ayudar a capturar estos parámetros de forma rápida y precisa en una gran área. Al integrar estos datos en modelos de análisis del ángulo crítico, los ingenieros pueden tener una mejor comprensión de la estabilidad de las pendientes y tomar decisiones informadas respecto a los riesgos geológicos y medidas de mitigación de riesgos.«Resistencias de la corteza y fallas a partir de mediciones de cono crítico: insights sobre el comportamiento de cuñas acrecionarias usando modelos de elementos distintos - NASA/ADS»
La teoría del cono crítico puede ser utilizada para mejorar la resiliencia de la infraestructura frente a peligros naturales al proporcionar una base para diseñar taludes estables. Al considerar el cono crítico, que es el talud más empinado que puede permanecer estable, los ingenieros pueden determinar el ángulo mínimo de un talud que puede soportar posibles peligros como terremotos o deslizamientos. Esta teoría ayuda a garantizar que la infraestructura se construya en taludes estables, minimizando el riesgo de fallas y aumentando la resiliencia frente a peligros naturales.«Complejo de subducción del Cenozoico tardío de Sicilia»
La teoría del cono crítico puede utilizarse para optimizar el diseño de infraestructura en áreas propensas a peligros naturales. Al entender la geometría de los taludes y analizar la estabilidad de los taludes bajo diferentes condiciones, los ingenieros pueden aplicar la teoría del cono crítico para diseñar estructuras que puedan resistir peligros naturales como deslizamientos de tierra, terremotos y huracanes. Esta teoría ayuda a determinar el ángulo ideal de los taludes y las dimensiones apropiadas de los elementos de infraestructura, mejorando su resiliencia y reduciendo el riesgo de fallas durante eventos naturales.«¿Cómo influye el espectro de tamaño de partículas en la segmentación de cuñas y la fluctuación del cono de prismas acrecionarios? - NASA/ADS»